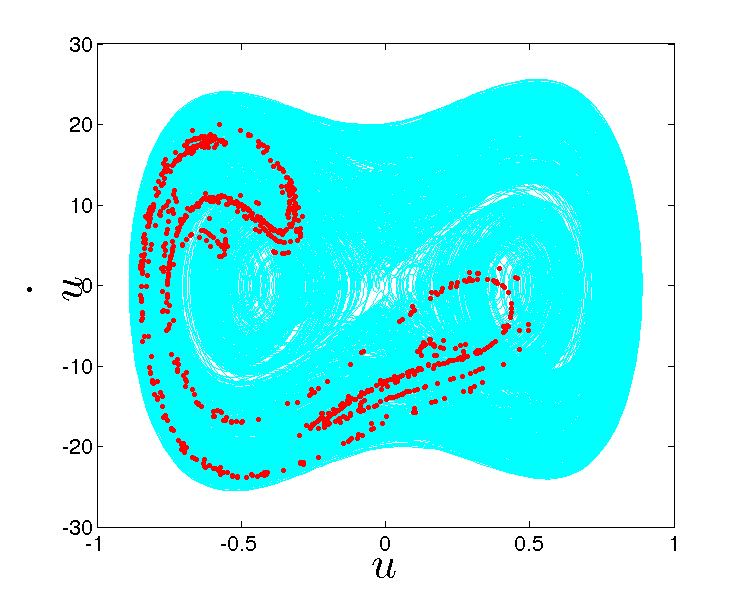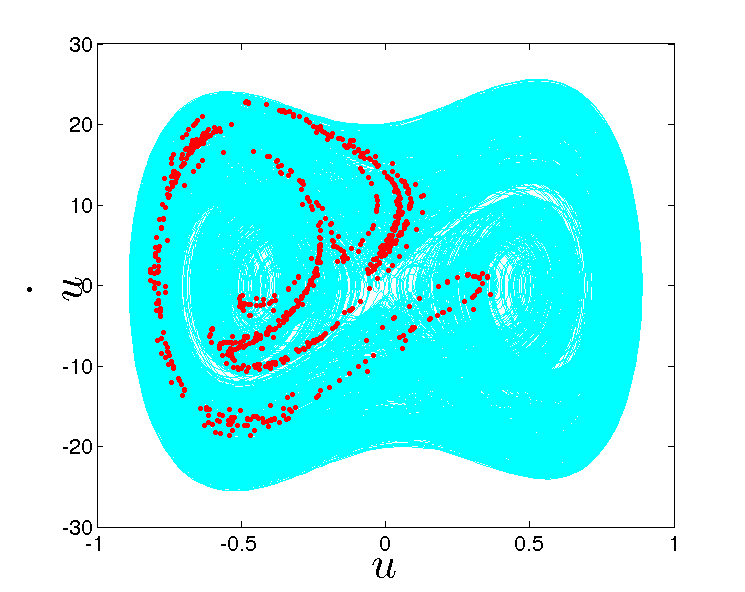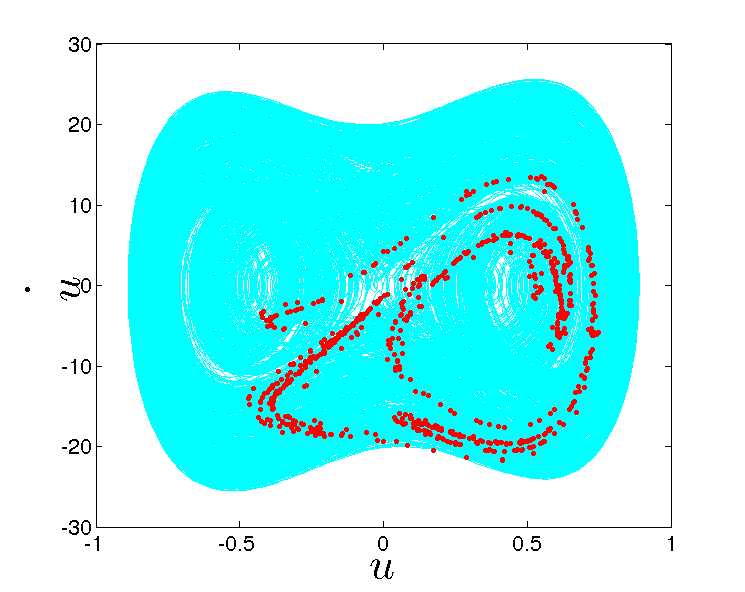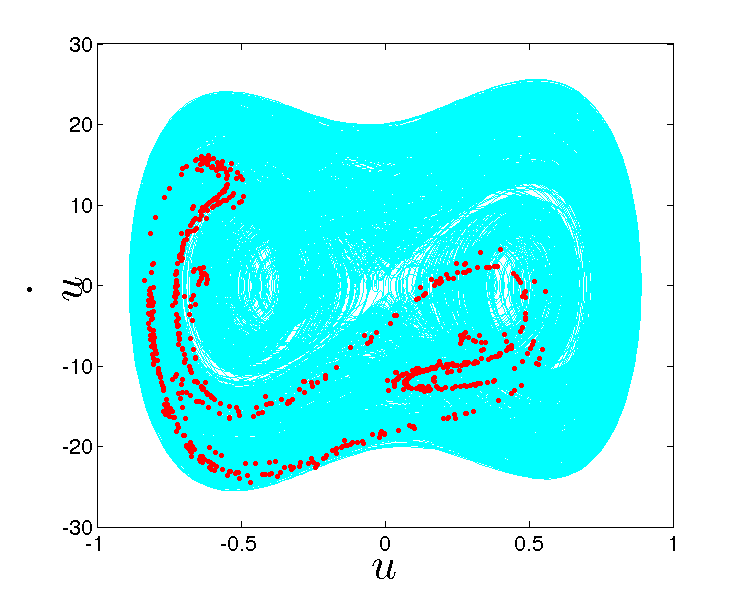
My research interests are primarily in stochastic mechanics and stochastic nonlinear dynamics. The origin of stochasticity lies in the inherent uncertainties that exists in nature; for example,   in the randomness in the loadings, such as earthquakes, wind and sea waves,  in the variations of the  micro-structure  in materials and in the variations of atmospheric conditions. An additional source of uncertainty lies in the insufficient knowledge in modelling or measuring nature. For example, simplifying assumptions in mathematical models, errors in acquiring measurement data also contribute to uncertainties. The focus of our studies is on modelling these uncertainties and quantifying how these uncertainties propagate through the analysis and manifest into the response.

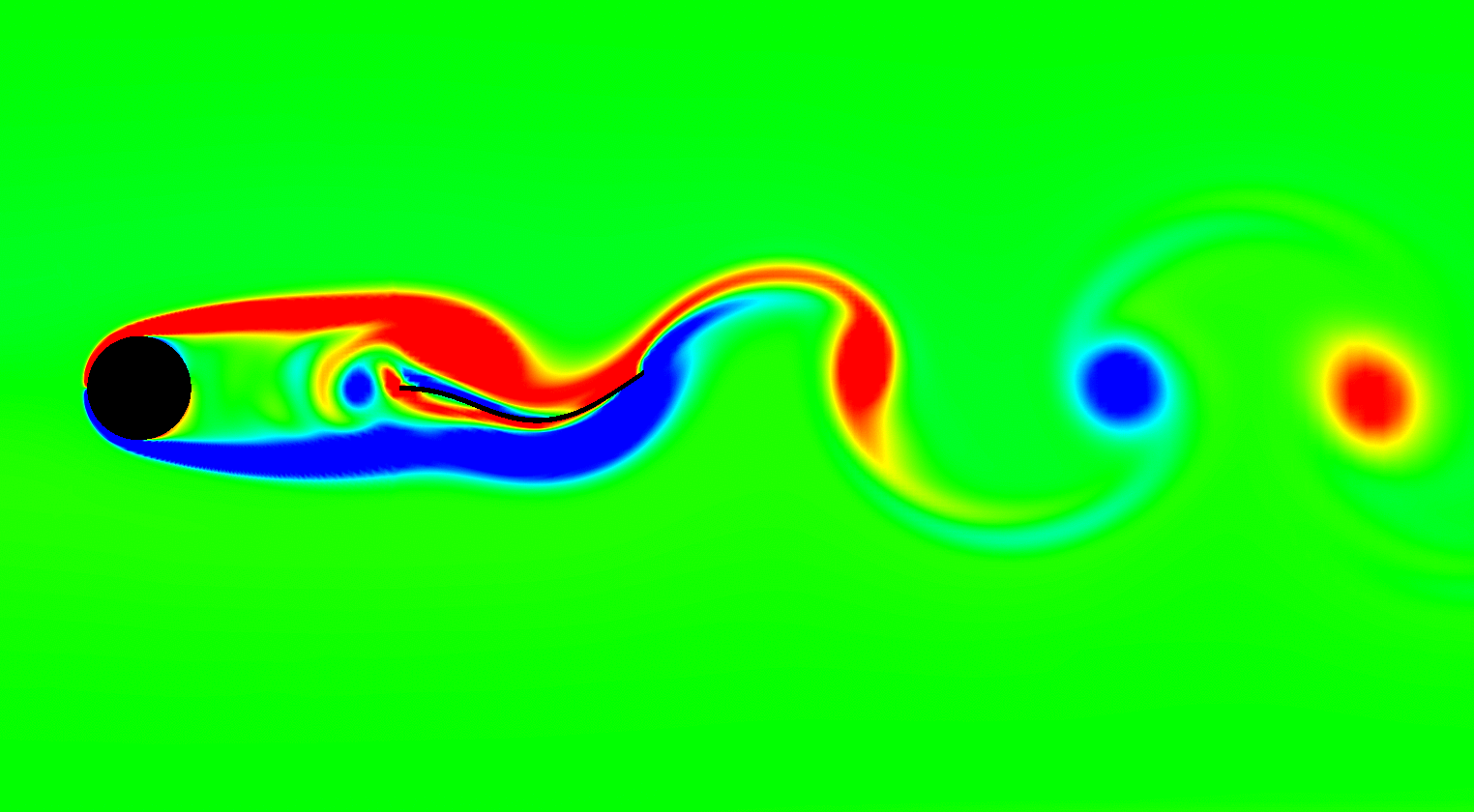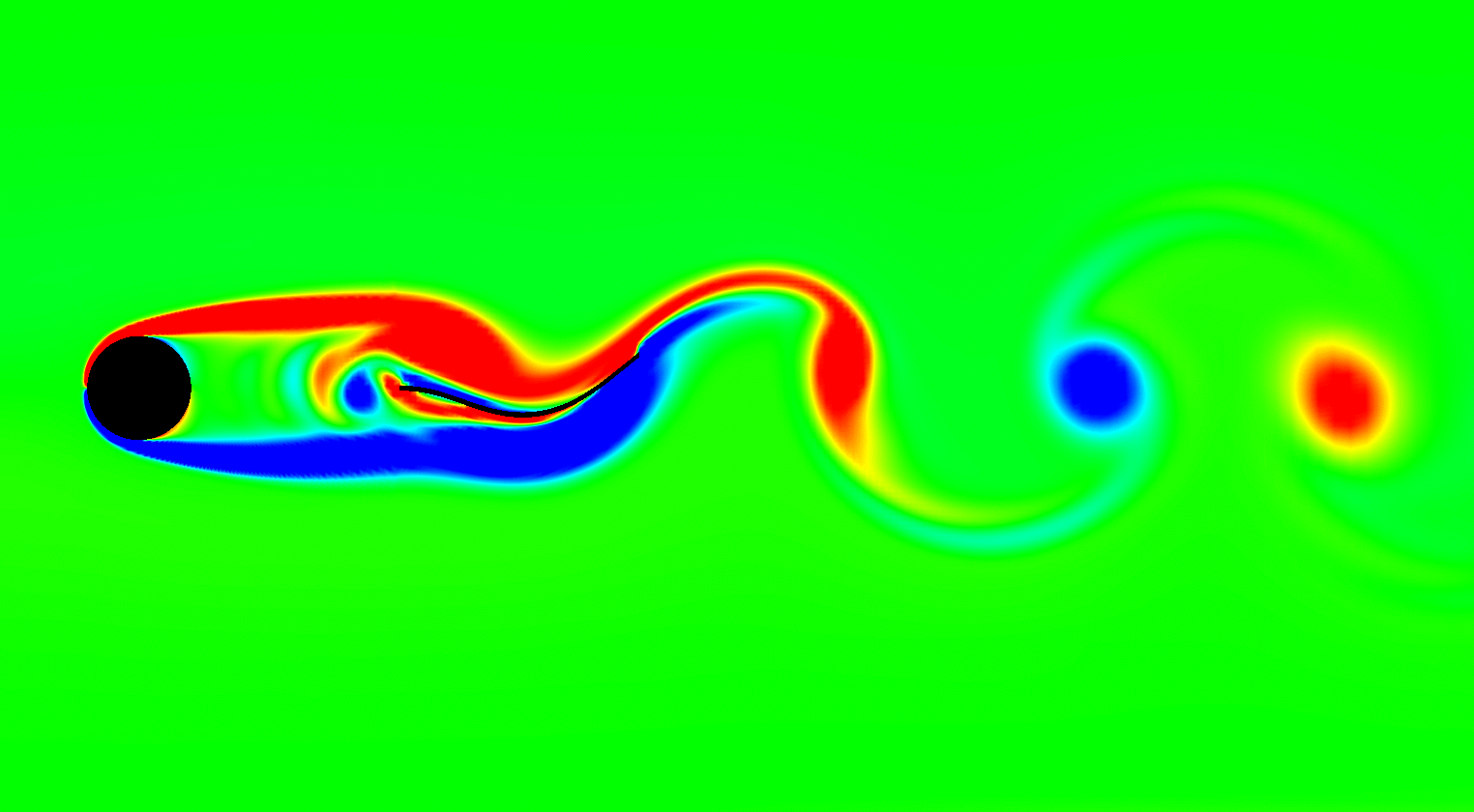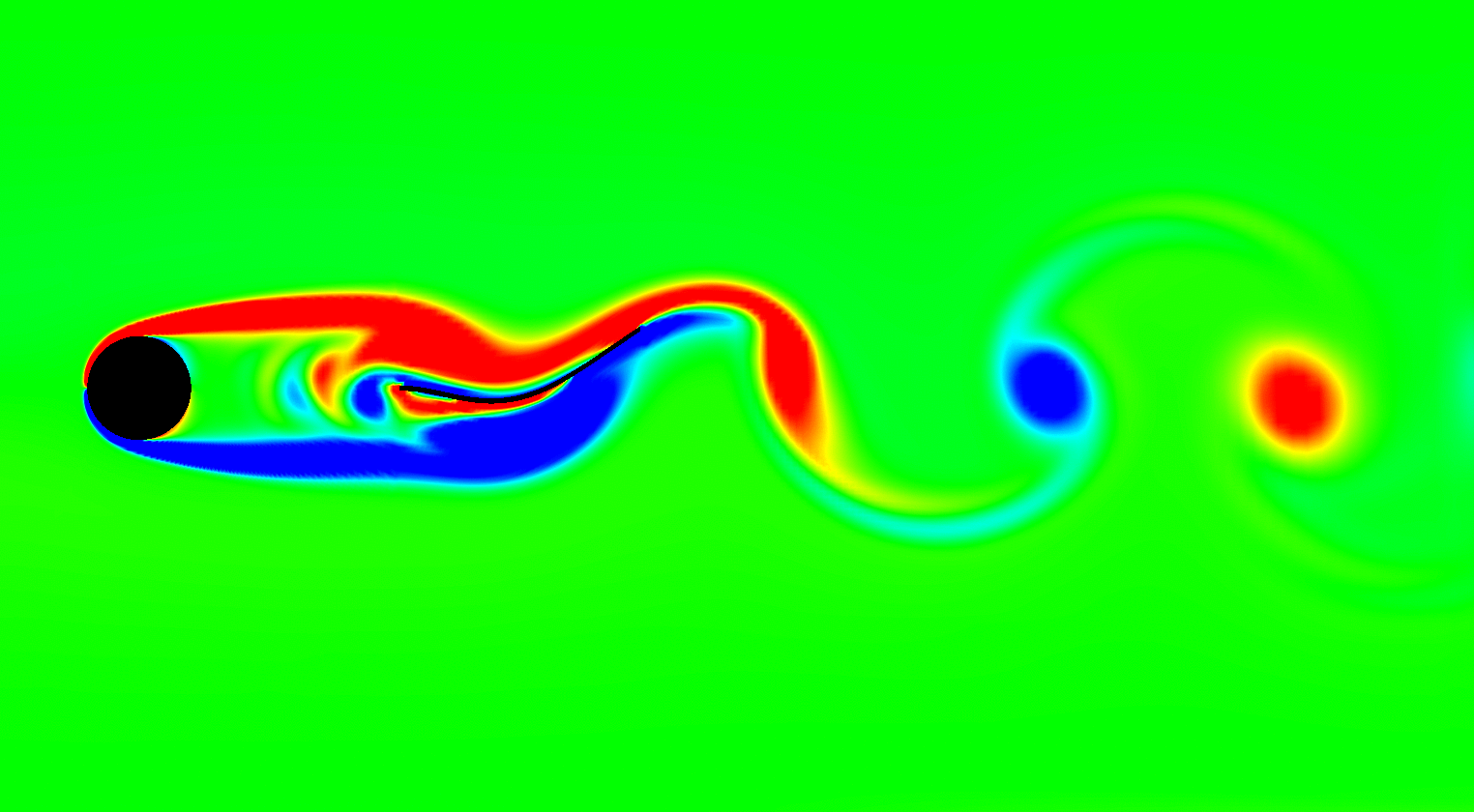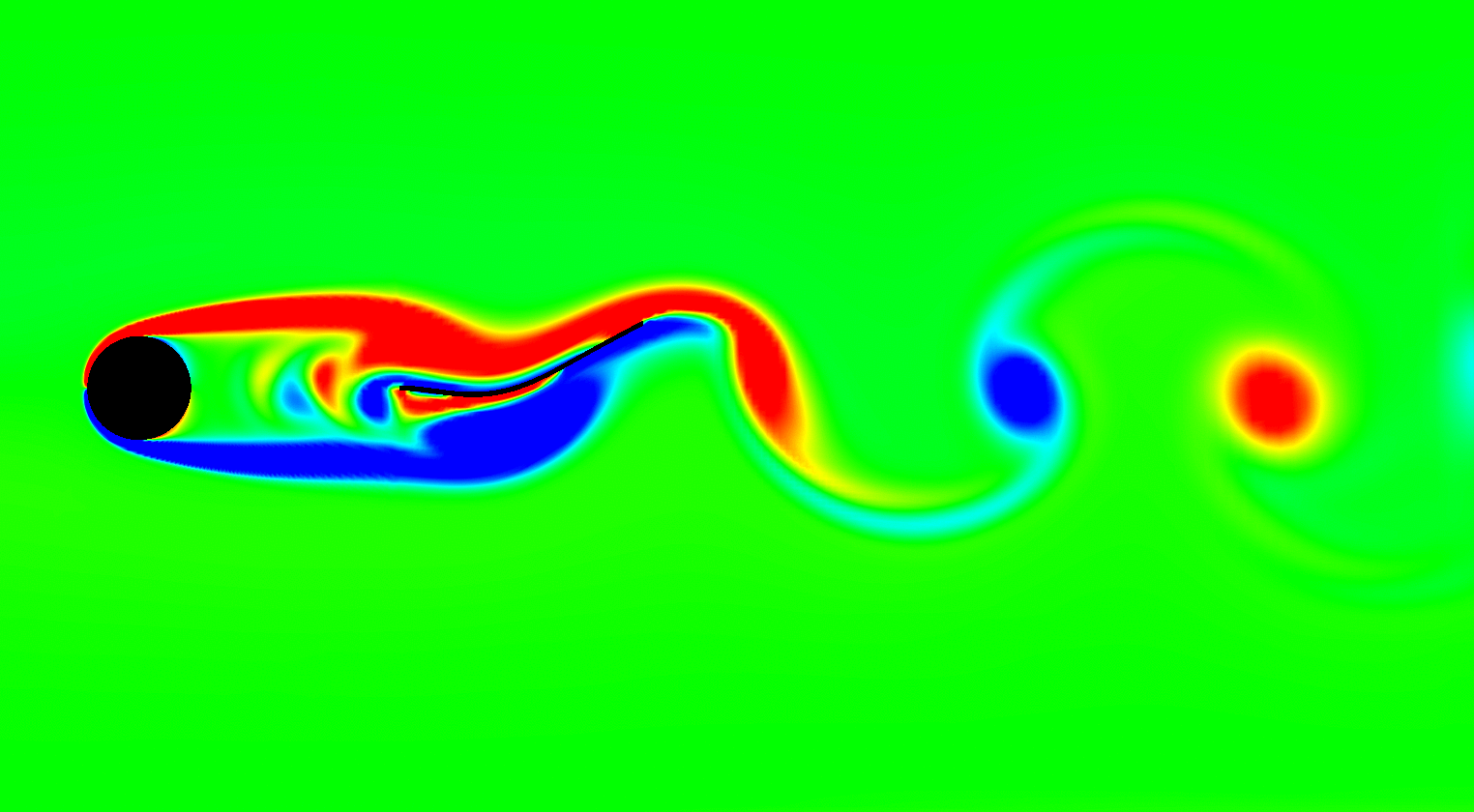
My interests in uncertainty analysis are primarily focussed on dynamical applications and vibrations with emphasis on understanding the nonlinear dynamical characteristics arising due to complexities resulting from geometric nonlinearities, coupled multi-physics problems (like fluid-structure interactions) and non-smooth dynamical systems.  I also investigate on problems involving uncertainty quantification in materials and composites. 

Complex Systems and Dynamics 

I am also leading the prospective Center on  Complex Systems and Dynamics  - an interdisciplinary initiative involving faculty members from different departments across the Institute. Here we focus on carrying out collaborative research on challenging large order dynamical systems that span disciplines of climate science, neuroscience, biomimetics, complex flows & social dynamics. Please visit here for more details.